Structurally Informed Spatial 3D Printing and Toolpath Generation for Cellular Structures in Architecture
The core of this research proposal focuses on optimizing FDM spatial 3D printing for construction parts with internal cellular structures. The study uses Finite Element Analysis (FEA) to guide material deposition based on stress values. The research further delves into the influence of cellular geometry, emphasizing the importance of individual cell details in dictating overall mechanical properties. The study aims to create structures for continuous printing by integrating Spatial Subdivision methods with Eulerian principles.
This research tackles the challenge of developing a continuous robotic 3D-printed toolpath. Using graph theory, the goal is to devise an effective toolpath strategy that prioritizes continuity, collision avoidance, and geometric considerations. The final objective is implementing state-space planning algorithms to generate a continuous toolpath, considering robotic orientation, structural constraints, and collision prevention.

Current construction methods are built with a combination of multiple materials that each have its own performative function. The purpose of this research is to explore the current construction methods and look at potential changes that additive manufacturing can bring that looks at the uniforming material performance as well as looking at how single and multiple materials impact the circular economy of the assembly.
Cells in nature are able to grow efficiently. This is evident in the way that plant leaves are able to effectively absorb sunlight and convert it into energy through photosynthesis. One reason for this efficiency is the way that cells are organized and structured within the leaf. The cells are arranged in a way that allows for maximum surface area, which is important for absorbing sunlight.
Additionally, the cells are also organized in a way that allows for efficient transport of nutrients and water throughout the leaf. These strategies can be applied to additive manufacturing, as the design of the cells can be optimized for the specific function of the part being produced. By studying the way that cells grow in nature and incorporating those principles into additive manufacturing, it is possible to create parts that are more efficient and perform better.
Unveiling the Geometric Influence: Exploring Cellular Properties and Spatial Subdivision for Enhanced Mechanical Efficiency and Aesthetic Appeal
The geometric properties of the cell play a critical role in determining the overall mechanical properties of the cellular structure. While the cellular structure defines the overall parts form, the single cell comprises the micro details that define the localized properties. These properties include the size and shape of each individual cell and their density and distribution. To achieve a variation in density, methods of Spatial Subdivision will be used to investigate creating the cellular density informed by the FEA analysis. Spatial Subdivision refers to a method by Kontiza. The approach used in this method involves defining the geometry of the space frame so that it can be subdivided by the centroid of tetrahedra and the midpoint of its edges. This subdivision process is recursive, allowing for a more efficient structural design. Factors such as ease of fabrication, structural integrity, and aesthetic considerations are considered to inform the final output. By optimizing the space frame through this subdivision approach, the resulting structure achieves improved efficiency in terms of its strength, fabrication process, and overall visual appeal. (Kontiza I., 2018).
This research is coupling the Spatial Subdivision method with Eulerian principles to develop the cellular structure for the continuous extrusion of material. While the Spatial Subdivision of tetrahedra showcases a successful method of creating a geometrical gradient, this method creates a disjointed structure not optimal for continuous printing. The achieve continuous extrusion, we propose to combine Eulerian principles in the design of the cell. Eulerian principles describe a method of subdivision where a triangle is subdivided into four triangles: an inscribed triangle and three triangles in the corners (see Figure 2b). A quadrangle is subdivided into one quadrangle and four triangles: an inscribed quadrangle and four triangles in the corners (see Figure 2b) (Madugula 2021). Using this technique of Eulerian subdivision, with minor tweaks, can be adapted to a spatial gradient of 5 cells (see Figure 2)
Toolpath Generation for Efficient Additive Construction: Integrating Functionally-graded Spatial Tool Pathing and State-space Planning Algorithms
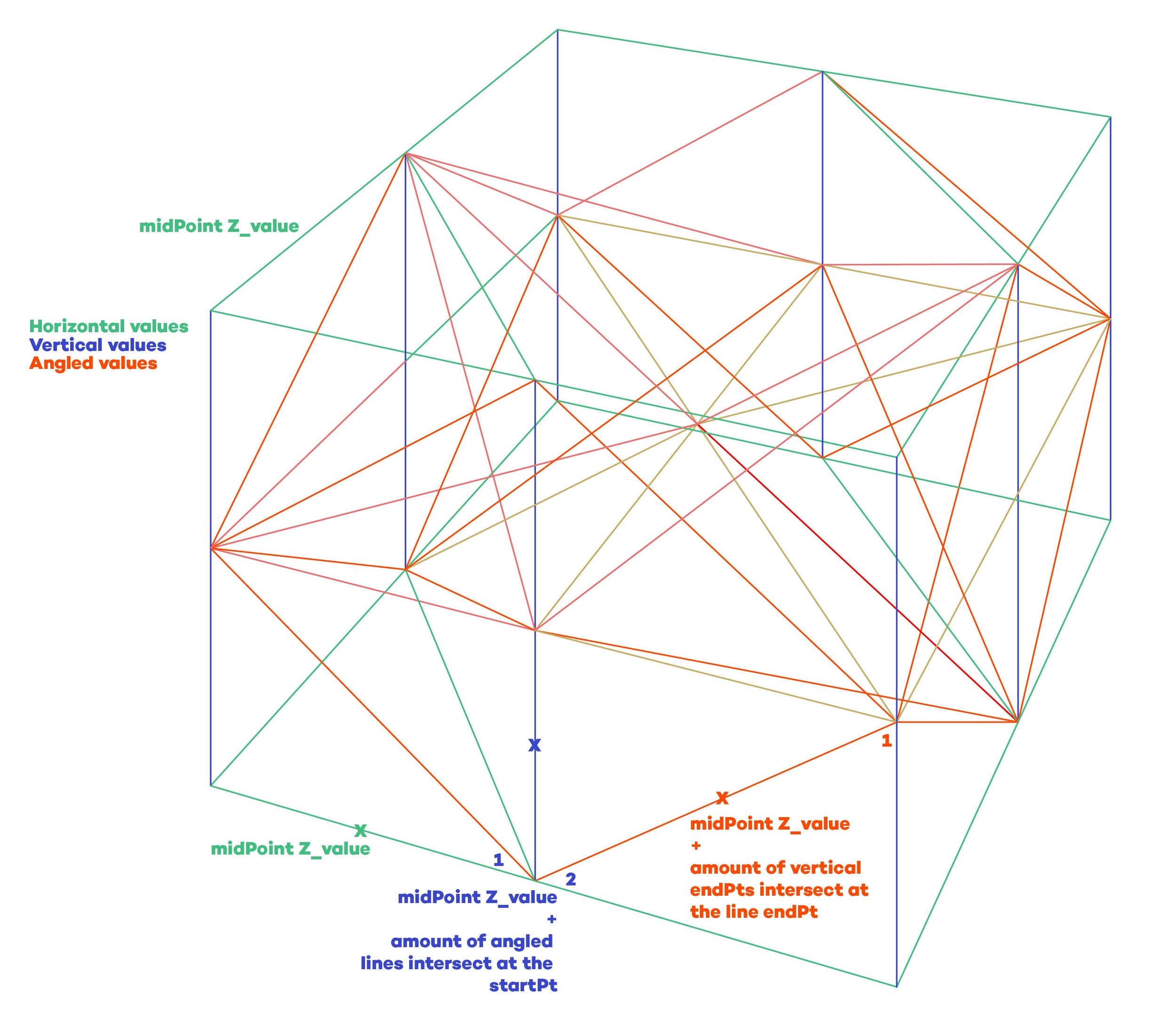
this research aims to solve is creating and optimizing a continuous robotic 3D printed toolpath from the cellular structure. Due to the cells in the part being unique to their localized forces, creating a continuous toolpath presents a challenge. Even using the Eulerian principles described previously, makes finding a continuous solution possible but very computationally intensive. Creating an efficient method of a continuous toolpath leverages graphs is a viable method for toolpath generation, as shown in the robotic additive construction of bar structures (Huang Y., 2021). A graph requires nodes and segments connecting the nodes, and in creating the cellular structure in the previous section, the nodes and segments have already been created. The next step is to develop the graph converting all nodes and segments in the generated cellular structure. Once all the node and segment connections are accounted for, we can use graph searching algorithms such as Breadth First Search and Depth First Search to find all the connected nodes and shortest paths, allowing for the generation of continuous toolpaths. While this method will produce toolpaths, the problem is that the current algorithm does not account for robotic orientation and collision. For that, the use of a ranking system and integration of state-space planning type algorithms will be used to create robotic movements that will satisfy non–collision and continuous extrusion conditions The reason for this choice of method is that state-space planning is a process used in designing programs to search for data or solutions to problems that satisfy requirements set forward in the program (Ghallab M, 2004). This objective aims to compute an efficient continuous toolpath that ranks each segment within the cellular structure in the toolpath(see Figure 2) based on the relation to the neighbor, the ability to print without collision, geometric, and structural constraints. (Huang Y. et al, 2021)
The image above on the left shows how the graph is structured for each node and the corresponding points to create an edge for the spatial object on the right, and the right image showcases the different line elements in the spatial test paths: horizontal, vertical, and angled edge. The categories are essential for determining the sequence of the print order so as not to collide with previously printed material. The elements' distinction helps define the logic for assigning weights to the edges and testing modified graph and greedy algorithms.
In developing a method of spatial extrusion in combination with FGAM the tool-path generation will attempt to be continuous. Continuous printing consists of depositing the filament in a single-extrusion without breaking the thermoplastic bead. The benefit of the continuous printing is the time-saving, and the superimposition of the material, which would distort the final print. We have found in previous testing that a buildup of material will converge at the location on the layer where the nozzle starts the extrusion as shown in the images below. The research will aim to mitigate the issues that are presented when printing non-continuously. Graph theory will be adopted to the methodology to computationally solve the spatial tool-path. Graph theory allows for the path to become a set of vertices and connections and the goal is to develop a path that is Eulerian. The Eulerian path is a graph where the edge between two vertices is visited only once and allows for revisiting of vertices e.g. semi-Eulerian as shown in the diagrams above.`